O campo magnético no centro de uma espira com diâmetro de vale .
- Qual é a corrente na espira?
- Um longo fio reto conduz a mesma corrente que você determinou no item a. A que distância do fio o campo magnético tem uma intensidade de ?
Passo 1
Faaaaaala, galera... Tranquileba??
Primeiro, vamos fazer o mais prudente: achar o campo magnético no centro de uma espira. Bora lá?
Seja uma espira ideal:
Então:
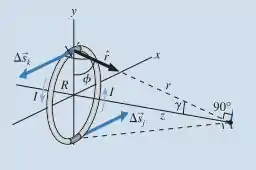
Vemos que as componentes em x e y se cancelam, sobrando somente em z.
Sabendo que a lei de bio-savart é:
Veja que:
Assim:
E que:
E também:
Assim ficando:
Integrando sobre toda a espira:
Concluímos que o campo magnético sobre uma espira é:
Como é no centro, logo . Assim ficando:
E já estamos com o pé na resposta, não?
Bora pro próximo passo!
Passo 2
Para a)
Pede-se a corrente I, logo:
Aplicando valores:
Passo 3
Para b)
Achemos novamente o campo magnético, mas agora para um fio que conduz uma corrente:
Sabemos que a lei de Bio-Savart é:
E para um fio muito longo, como:
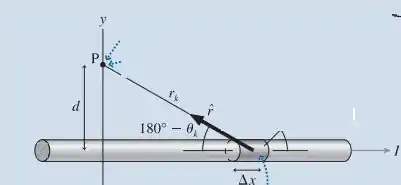
Temos que:
E:
Assim:
Sendo um fio muito longo, logo:
Logo:
De integral simples. Assim, o campo elétrico a uma distancia d sobre um fio longo que passa uma corrente é:
Pede-se d, assim:
Aplicando valores:
Resposta
Para a)
Para b)