Qual é o campo magnético no centro da espira da FIGURA P33.48?
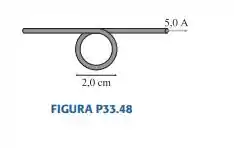
Passo 1
Faaaaaala, galera... Tranquileba??
Seja uma espira ideal:
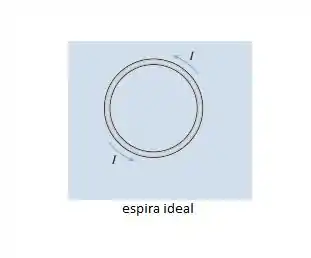
Então:
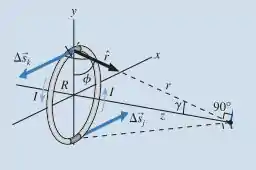
Vemos que as componentes em x e y se cancelam, sobrando somente em z.
Sabendo que a lei de bio-savart é:
Veja que:
Assim:
E que:
E também:
Assim ficando:
Integrando sobre toda a espira:
Concluímos que o campo magnético sobre uma espira é:
Sendo dentro da espira , assim:
E para o campo elétrico no fio:
E podemos usar o princípio da superposição.
E já estamos com o pé na resposta, não?
Bora pro próximo passo!
Passo 2
Assim:
Passo 3
Aplicando valores:
Concluímos que: