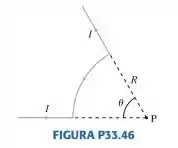
1. Obtenha uma expressão para o campo magnético no centro (ponto P) do arco circular da FIGURA P33.46.
2. Seu resultado está em concordância com o campo magnético criado por uma espira de corrente quando ?

Faaaaaala, galera... Tranquileba??

Para a)

Temos pela lei de Bio-Savart que:

Daí temos que:

Se:

E:

Assim ficando, considerando a perpendicularidade:

Integrando, considerando na distância P :

Tomando o intervalor de integração de portanto:

Fácil, né? Que nada ksksk mas é basicamente conceitos.

Bora para o item b