Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 33.Exercícios e Problemas - Ex. 51
O campo magnético da Terra, com um momento de dipolo magnético de , é gerado por correntes no interior do ferro fundido do núcleo externo da Terra (o núcleo interno é de ferro sólido). Como um modelo simples, considere uma espira de corrente feita com um “fio” de ferro derretido com 1.000 km de diâmetro. O diâmetro da espira, medido entre os centros dos “fios”, é de 3.000 km. a. Qual é a
- intensidade de corrente na espira?
- Qual é a densidade de corrente J na espira?
- Para decidir se esta é uma densidade de corrente grande ou pequena, compare-a à densidade de corrente correspondente a uma corrente de 1,0 A em um fio com 1,0 mm de diâmetro
Passo 1
Faaaaaala, galera... Tranquileba??
Fazendo um desenho do que o enunciado queer nos passar, temos:
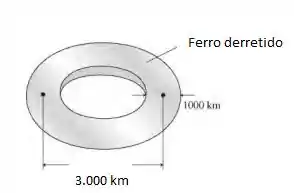
Para a)
Sabemos que:
Sendo a área da volta/ loop
Dado a área A, isto é: dado o raio já temos a área, não? Também dado o momento de dipolo magnético. Então:
Bora pro próximo passo e próximo item?!
Passo 2
Para b)
Sabemos que a densidade de corrente é na espira, logo devemos tomar somente sua seção transversal, que vemos que é de diâmetro
Logo, já tendo tudo (dessa vez com o fio de ferro derretido):
Pronto para o próximo item?
Passo 3
Cá estamos
Para c)
Da equação já dita antes:
Aplicando os valores dados:
Vemos que . A corrente da terra é grande, mas a corrente de densidade é muito pequena
Resposta
Para a)
Para b)
Para c)