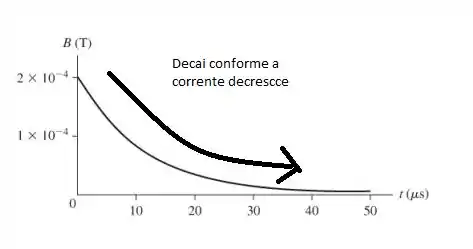
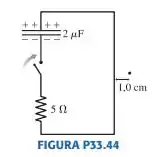
O capacitor na FIGURA P33.44 está carregado a 50 V. O interruptor é fechado em . Desenhe um gráfico que represente a intensidade do campo magnético em função do tempo na posição indicada pelo ponto. No gráfico, indique a intensidade máxima do campo e uma escala numérica apropriada para o eixo horizontal.
Passo 1
Faaaaaala, galera... Tranquileba??
Primeiro precisamos achara equação para o descarregamento da corrente, para assim sim podermos aplicar ao campo magnético.
Assim, a corrente de descarregamento é dada deste modo:
Usando a lei de Kirchoff, isto é:
Quando o circuito é fechado, como neste circuito. Assim:
Sabemos que:
Logo:
Sabemos que a carga total no capacitor é:
Logo:
Façamos:
Logo:
Assim:
O limite de integração para U, que é a corrente, é da corrente inicial até o final, e do tempo e é de 0 até o tempo determinado, isto é, t’:
Procurávamos a corrente, então:
Pelo que demos antes sobre , concluímos que:
E já estamos com o pé na resposta, não?
Bora pro próximo passo!
Passo 2
Aplicando os valores dados:
Sendo a corrente gerada no fio
Passo 3
Definamos a o campo elétrico a uma distancia d de um fio. Saca só:
Sabemos que a lei de Bio-Savart é:
E para um fio muito longo, como:
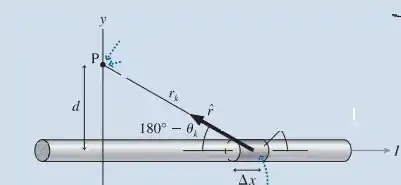
Temos que:
E:
Assim:
Sendo um fio muito longo, logo:
Logo:
De integral simples. Assim, o campo elétrico a uma distância d sobre um fio longo que passa uma corrente é:
Aplicando a nossa corrente já conhecida:
Aplicando os valores:
Fazendo um gráfico, obtemos:
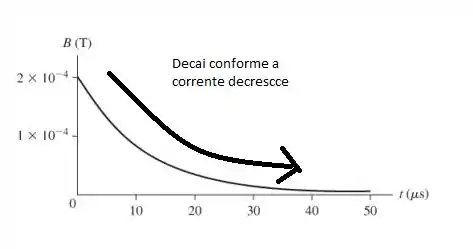
Resposta