Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 12.Problemas - Ex. 1
Um capacitor de placas paralelas é formado por dois discos de raio separados por uma distância , no vácuo. As placas estão ligadas a um gerador AC que produz uma carga no capacitor . Admita que o campo entre as placas é uniforme, desprezando fuga de linhas de corrente, e tome o eixo ao longo do eixo do capacitor. Calcule o campo entre as placas, a uma distância do eixo.
Passo 1
Primeiro vamos desenhar um esquema do capacitor:
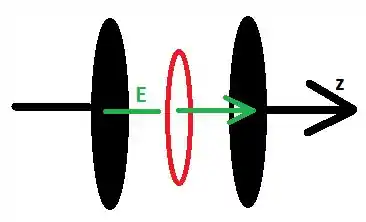
Como o campo elétrico é suposto uniforme entre as placas, temos que
Temos que é a densidade superficial de carga acumulada nas placas:
Como , segue que
Portanto,
Passo 2
Agora vamos escrever a lei de Ampère com a correção de Maxwell:
Note que podemos definir o fluxo elétrico como
Assim,
onde
é a corrente de deslocamento, uma corrente fictícia que aparece devido a variação do fluxo elétrico no tempo.
No nosso problema, não temos corrente real entre as placas, de modo que . Vamos considerar um circuito (desenhado em vermelho) de raio . Vamos calcular o fluxo elétrico que atravessa esse circuito:
Como :
Logo,
Passo 3
Assim,
Portanto, temos que
Assim, vemos que o campo magnético deve ser tangencial ao circuito vermelho de raio , de modo que
Assim,
Logo, para :
Escrevendo vetorialmente, temos que
Passo 4
Agora vamos olhar para um circuito vermelho com . Nesse caso, continuamos a ter
Mas agora, para calcular o fluxo, devemos lembrar que o campo só existe até . Portanto,
Assim,
Portanto, para :
Com isso, podemos escrever:
O campo elétrico variável no tempo é responsável por criar um campo magnético!