Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 32.Exercícios e Problemas - Ex. 76
Os capacitores da FIGURA PD32.76 estão carregados, e o interruptor fecha em t 0 s. Em que instante a corrente do resistor de 8 decai para a metade do valor que tinha imediatamente após o interruptor ter sido fechado?
Passo 1
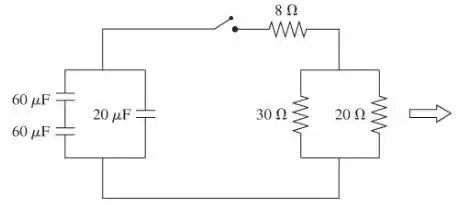
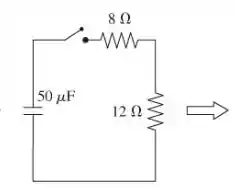
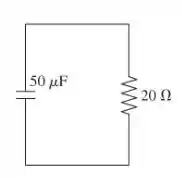
A figura mostra como simplificar o circuito na Figura P32.76 usando as leis dos resistores em série e paralelo e as leis dos capacitores em série e em paralelo.
Passo 2
Os resistores de 30 Ω e 20 Ω estão em paralelo e são equivalentes a um resistor de 12 Ω. Este resistor de 12 Ω está em série com o resistor de 8 Ω de modo que a resistência equivalente do circuito R eq = 20 Ω. Os dois capacitores de 60 μF estão em série produzindo uma capacitância equivalente de 30 μ F. Este capacitor de 30 μ F está em paralelo com o capacitor de 20 μF, então a capacitância equivalente C eq do circuito é 50 μ F. A constante de tempo deste circuito é
A corrente devida aos três capacitores através do resistor equivalente de 20 Ω é a mesma que através do resistor de 8 Ω resistor. Então, a tensão no resistor de 8 Ω segue a equação de decaimento . Para