Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 17.Exercício - Ex. 67
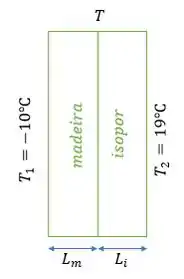
Um carpinteiro constrói a parede externa de uma casa usando uma camada de madeira com 3,0 cm de espessura e uma camada de isopor com espessura de 2,2 cm na superfície interna da parede. A madeira possui e o isopor possui . A temperatura da superfície interna da parede é igual a e a temperatura da superfície externa é . a) Qual é a temperatura na superfície da junção entre a madeira e o isopor? b) Qual é a taxa de transferência de calor por metro quadrado através da parede?
Passo 1
Há uma diferença de temperatura na superfície entre a madeira e o isopor, por isso temos condução de calor através dessa superfície.
Vamos chamar a temperatura na interface entre a madeira e o isopor de T.
A taxa de transferência de calor em cada material é dada por
Taxa de transferência de calor através da madeira:
Taxa de transferência de calor através do isopor:
No estado estacionário, o calor não se acumula em nenhum dos materiais. A mesma quantidade de calor deve passar pelos dois materiais, então as taxas de transferência de calor devem ser iguais (esse é o caso de uma associação em série de condutores de calor):
Passo 2
(a) Isso implica que, substituindo as fórmulas:
Isolando :
E substituindo os valores que temos:
A temperatura na junção é muito mais próxima em valor a do que a . O isopor tem
muito grande, portanto, é necessário um gradiente de temperatura maior para que a madeira estabeleça a mesma corrente de calor.
Passo 3
(b) O fluxo de calor por metro quadrado é
Podemos calcular isso para a madeira ou isopor; os resultados devem ser os mesmos.
Passo 4
Madeira:
Passo 5
Isopor:
deve ser o mesmo para ambos os materiais e nossos resultados numéricos mostram isso. Ambos os materiais são bons isoladores e o fluxo de calor é muito pequeno.