Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 17.Exercício - Ex. 66
Uma das extremidades de uma barra metálica isolada é mantida a , e a outra extremidade é mantida a por uma mistura de gelo e água. A barra tem de comprimento e uma seção reta com área igual a . O calor conduzido pela barra produz a fusão de de gelo em . Ache a condutividade térmica do metal.
Passo 1
Bora lá galera. Pra começar, veja que a questão pede a condutividade térmica. Então vamos puxar uma fórmula em que essa constante apareça. Se usarmos a fórmula do livro:
Vemos que ela aparece aí! É a letrinha . Ok, não temos uma expressão pra derivar, mas não precisamos, basta considerar uma taxa de condução de calor média:
E isolando , temos:
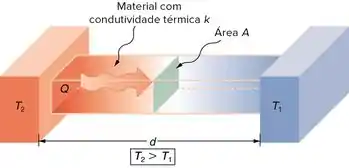
Do nosso enunciado, temos:
- Comprimento da barra
- Área de seção reta da barra
- Tempo da condução de calor
- Temperatura da extremidade quente
- Temperatura da extremidade fria
O que já nos fornece bastante pra esse cálculo! Substituindo:
Mas quem é ? Bora descobrir
Passo 2
Pra achar vamos olhar o enunciado com calma. Ele diz que a extremidade fria é uma mistura de água e gelo a . Cara, isso significa que se dermos calor pra essa mistura, não vamos ter mudança de temperatura! Todo calor fornecido será usado para a transição de fase! Quando é assim, vale a fórmula:
Como o enunciado deu a massa de água que foi fundida, ou seja, quanto de gelo derreteu e sendo uma constante conhecida:
Vamos ter:
Substituindo isso na fórmula do Passo :
Como:
Temos:
Feshow!