Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 3- Ed: 6º - Capítulo 34.1 - Ex. 13

O cátodo usado pelos alunos no experimento descrito no Problema 12 é construído a partir de um dos seguintes metais:

Determine qual metal compõe o cátodo usando os mesmos dados do Problema 12. (a) Usando um programa de planilha eletrônica ou calculadora gráfica, plote Kmax versus frequência. (b) Use o gráfico para estimar o valor da função de trabalho com base nos dados dos alunos. (Nota: Você pode usar um recurso do seu programa de planilhas ou calculadora gráfica para obter o melhor ajuste linear aos dados.) (C) Qual metal foi provavelmente usado no catodo em seu experimento?

Passo 1

(a) Da equação de Einstein, a gente tem:

K m a x = h f - ϕ

Podemos fazer uma comparação com a equação da reta:

y = a x + b

Assim, y = K m a x , x = f e a = h e b = - ϕ . Dessa forma, podemos ligar os pontos da tabela com uma reta e calcular o coeficiente angular dela, que será o nosso comprimento de onda de Compton experimental!

Passo 2

Passando todos os valores de K m a x para joules, é só multiplicar o valor por 1,6 ∙ 10 - 19 :

0,36   e V = 5,76 ∙ 10 - 20   J

0,199   e V = 3,18 ∙ 10 - 20   J

0,156   e V = 2,5 ∙ 10 - 20 J

0,117   e V = 1,87 ∙ 10 - 20   J

0,062   e V = 9,92 ∙ 10 - 21   J

Em x teremos valores de f = c λ e em y , de K m a x . Sendo assim, olhando para a tabela, o gráfico será:

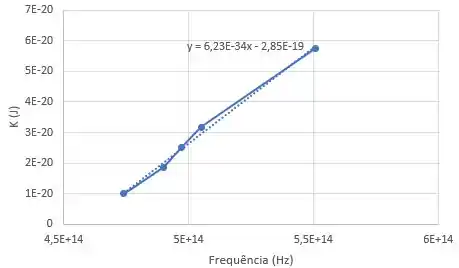
Fazendo a aproximação linear, chegamos na equação do gráfico ali:

y = 6,23 ∙ 10 - 34 x - 2,85 ∙ 10 - 19

Passo 3

(b) Então, olhando para essa equação, vemos que b = - 2,85 ∙ 10 - 19 e, como vimos, b = - ϕ → ϕ = 2,85 ∙ 10 - 19   J . Para passar para eletron volt, vamos dividir por 1,6 ∙ 10 - 19 :

ϕ = 2,85 ∙ 10 - 19 1,6 ∙ 10 - 19 = 1,78   e V

Passo 4

(c) Olhando para os valores associados aos metais, vemos que o valor encontrado na letra anterior chega mais perto do valor do césio!

Resposta

(a)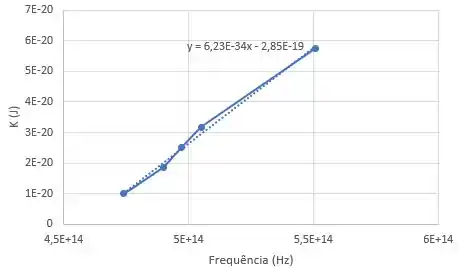

(b) ϕ = 1,78   e V

(c) Césio.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A função trabalho do tungstênio é 4,50e V . Calcule a velocidade dos elétrons mais rápidos ejetados da superfície de uma placa de tungstênio quando fótons com uma energia de 5,80e V incidem na placa.
Em um experimento do efeito fotoelétrico usando uma placa de sódio, é encontrado um potencial de corte de 1,85V para um comprimento de onda de 300n m e um potencial de corte de 0,820V para um comprime
Um feixo luminoso incide na superfície de uma placa de sódio, produzindo uma emissão fotoelétrica. O potencial de corte dos elétrons ejetados é 5,0V e a função trabalho do sódio é 2,2e V . Qual é o co
A luz solar pode ejetar elétrons da superfície de um satélite em órbita, carregando-o eletricamente; os projetistas de satélites procuram minimizar este efeito através de revestimentos especiais. Supo
A eficiência relativa de uma superfície de césio (cuja função trabalho é 1,80e V ) é 1,0 ⋅ 10 - 16 , o que siginifca que, em média, um eletron é ejetado para cada 10 16 fótons que incidem na superfíci