Em um certo instante, uma função de onda depende da posição conforme está mostrado na figura 5-20.
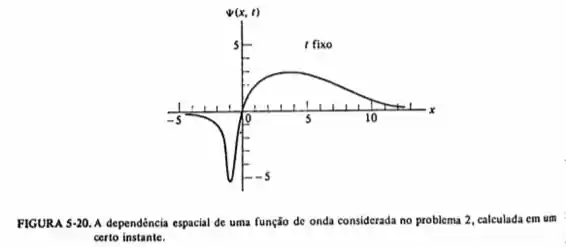
a) Se fosse feita uma medida que possa localizar a partícula associada em um elemento do eixo nesse instante, onde seria maior a probabilidade de encontrá-la?
b) Onde seria menor esta probabilidade?
c) As chances de que ela seja encontrada em qualquer valor positivo do eixo seriam melhores do que as chances de que seja encontrada em qualquer valor negativo?
Passo 1
Fala galerinha, beleza?
O enunciado forneceu o gráfico da função de em função da posição . Tome muito cuidado antes de responder o problema! Lembre-se que segundo a interpretação estatística da mecânica quântica, o quadrado da função de onda fornece a densidade de probabilidade. Desta forma, as regiões em que a função de onda é negativa vão contribuir.
Nesse caso, o maior valor em módulo de ocorre para . Essa vai ser a região de maior probabilidade de encontrar a partícula!
A seguir fazemos um esboço da :
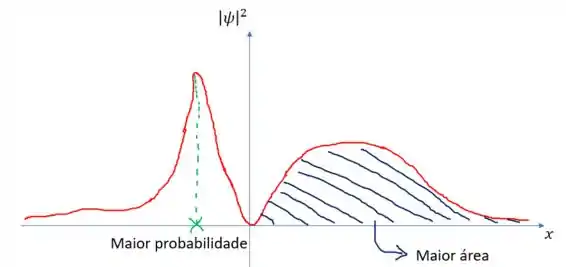
A região com maior probabilidade de encontrar a partícula é aquela em a curva atinge seu máximo. O pico negativo de vira um pico positivo de .
A região de menor probabilidade é aquela em se anula. Nesse caso, .
Passo 2
Agora vamos responder o item (c)!
A probabilidade de a partícula estar em uma posição positiva é dada pela área abaixo da curva pintada em azul. Como a área para é maior que para , existe uma probabilidade maior de a partícula estar em uma posição positiva!
Resposta
Desenho.