O circuito exibido na Figura P21.72 foi configurado em um laboratório para medir uma capacitância desconhecida C em série com resistência R = 10,0 MW alimentada por uma bateria cuja FEM é 6,19 V. Os dados apresentados na tabela são as tensões medidas no capacitor como função do tempo, onde t = 0 representa o instante no qual a chave é colocada na posição b. (a) Faça um gráfico de ln e/DV como função de t e execute um ajuste linear de mínimos quadrados aos dados. (b) A partir da inclinação de seu gráfico, obtenha um valor para a constante de tempo do circuito e um valor para a capacitância
Passo 1
E aiii gente, tudo bom com vocês?
Então vamos resolver essa questão bem legal aqui e passo a passo pra gente tirar 10 na provinha!
Vamo lá!
Letra a:
O gráfico será:
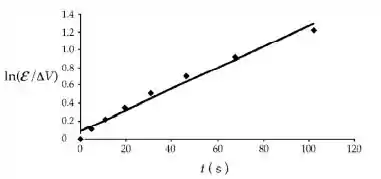
Passo 2
A partir dos valores:
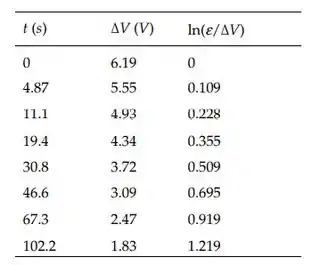
A melhor equação é então,
Passo 3
Letra b:
Resposta
- e