Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Exercício - Ex. 7
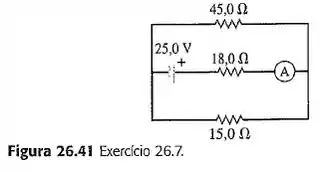
Para o circuito na Figura 26.41, determine a leitura do amperímetro ideal, caso a bateria tivesse uma resistencia interna de .
Passo 1
E aí, galera, belezinha?
Bom, primeiro, faça o máximo possível de redução paralela em série.
Os resistores e estão em paralelo; portanto, primeiro reduza-os a uma única resistência equivalente. Em seguida, vamos encontrar a resistência em série equivalente do circuito.
Passo 2
Então, determinando a leitura do amperímetro ideal, caso a bateria tivesse uma resistencia interna de , temos que:
E
Passo 3
A resistência equivalente total é:
A Lei de Ohm nos dá que:
O circuito parece complicado até que percebamos que os resistores e estão em paralelo.
Resposta
Exercícios de Livros Relacionados
No circuito da Figura 26.47, um resistor de 20Ω está imerso em 100 g de água pura, contida em um recipiente de isopor isolante. Supondo que a água esteja inicialmente a 10,0 ° C , quanto tempo levará
No circuito indicado na Figura 26.46, a voltagem através do resistor de 2,0Ω é de 12,0V . Indique a fem da bateria e a corrente que passa pelo resistir de 6,0Ω ?
Calcule a resistência equivalente do circuito indicado na Figura 26.42 e determine a corrente que passa em cada resistor. A bateria possui resistência interna desprezível.
No circuito indicado na Figura 26.48, a taxa de dissipação da energia elétrica de R 1 é igual a 20,0 W. (a) Detemine R 1 e R 2 . (b) Qual é a fem da bateria? (c) Ache a corrente que passa por R 2 e pe