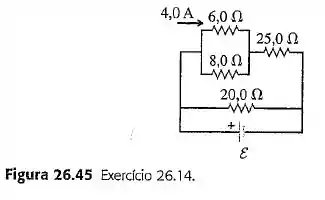
Considere o circuito indicado na Figura 26.45. A corrente que passa pelo resistor de 6,0Ω é igual a 4,0Ω , no sentido indicado. Quais são as correntes que passam pelo resistores de 25,0Ω e 20,0Ω ?

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Exercício - Ex. 14

Considere o circuito indicado na Figura 26.45. A corrente que passa pelo resistor de é igual a , no sentido indicado. Quais são as correntes que passam pelo resistores de e ?

Passo 1

Aplicaremos a lei de Ohm a cada resistor.

Para resistores em paralelo, as tensões são as mesmas e as correntes são adicionadas. Para resistores em série, as correntes são as mesmas e as tensões aumentam.

Passo 2

Pela lei de Ohm, a queda de tensão no resistor de é . A queda de tensão no resistor de é a mesma, pois esses dois resistores são conectados em paralelo. O atual através do resistor de é então . A corrente através do resistor de é a soma destas duas correntes: . A queda de tensão no resistor de é , e a queda de tensão total na parte superior do circuito é de , que também é a tensão a cair através do resistor de . A corrente através do resistor de é então .

Passo 3

A corrente total através da bateria é . Observe que não precisamos calcular a fem da bateria.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Prove que, quando dois resistores são ligados em paralelo, a resistencia equivalente da combinação é sempre menor do que a resistencia de qualquer um dos resistores. (b) Generalize o resultado do item

Um equipamento possui um resistor X que se projeta de uma abertura lateral. Esse resistor é conectado a outros três resistores, como indica a Figura 26.38. Um ohmímetro conectado através de a e b regi

A potencia máxima especificada sobre o resistor é a maior potencia que pode ser dissipada no resistor, sem que ele atinja a temperatura demasiadamente elevada. (a) Se a potencia máxima que um resistor

Calcule a resistência equivalente do circuito indicado na Figura 26.43 e determine a corrente que passa em cada resistor. A bateria possui resistência interna desprezível.