Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Exercício - Ex. 21
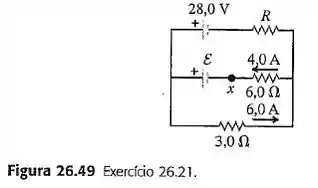
No circuito indicado na Figura 26.49, calcule (a) a corrente no resistor R; (b) a resistência R; (c) a fem desconhecida . (d) Se o circuito fosse cortado no ponto , qual seria a nova corrente no resistor R?
Passo 1
E aí galera, aqui vamos aplicar a regra de ponto de Kirchhoff no ponto para encontrar a corrente através de.
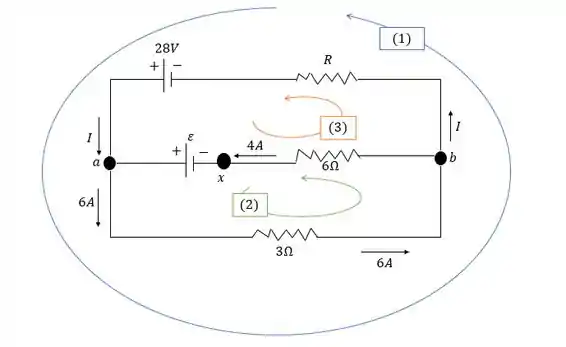
Aplique a regra de loop de Kirchhoff a loops (1) e (2) mostrados na Figura a seguir, para calcular e .
Viaje ao redor de cada loop na direção mostrada.
Passo 2
- Aplicando a regra de ponto de Kirchhoffs ao ponto :
- Aplicando a regra de loop de Kirchhoff ao loop (1):
- Aplicando a regra de loop de Kirchhoff ao loop (2):
- Se o circuito for interrompido no ponto x, não haverá corrente no resistor . Agora existe apenas um único caminho atual e podemos aplicar a regra de loop a esse caminho.
Então:
(na direção mostrada no diagrama).
Passo 3
Isso implica que:
Passo 4
Pode verificar se a regra do loop é satisfeita para o loop (3), como uma verificação do nosso trabalho:
portanto, a regra do loop é satisfeita para esse loop.
Passo 5
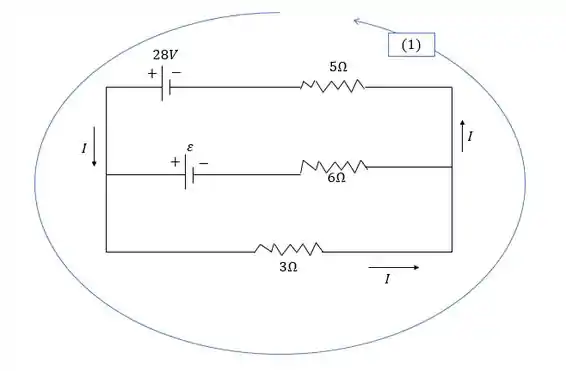
Para calcular a nova corrente do resistor fazemos:
Isso implica que:
A quebra do circuito em remove a fem de do circuito e a corrente através do
resistor é reduzido.