Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 32.Exercícios e Problemas - Ex. 60
Para o circuito mostrado na FIGURA P32.60, determine a corrente
e a diferença de potencial em cada resistor. Para facilitar a leitura,
apresente seus resultados em uma tabela.
Passo 1
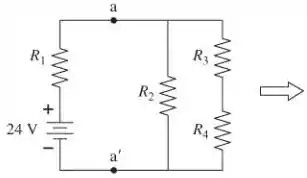
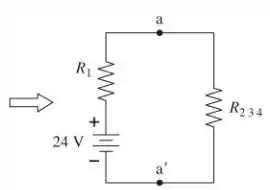
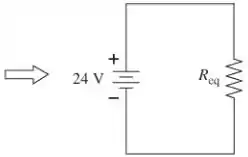
A figura mostra como simplificar o circuito da Figura P32.60 usando as leis das resistências em série e em paralelo. Rotulamos os resistores como R1 = 6 Ω, R2 = 15 Ω, R3 = 6 Ω e R4 = 4 Ω. Reduzindo o circuito a um resistência equivalente única Req, vamos inverter o procedimento e “construir” o circuito usando a lei do loop e a lei de junção para encontrar a diferença de corrente e potencial de cada resistor.
Passo 2
e são combinados para obter = 10 Ω, e então e são combinados para obter
do último circuito,
Assim, a corrente através da bateria e é = 2 A e a diferença de potencial através de é
Passo 3
À medida que reconstruímos o circuito, notamos que os resistores em série devem ter a mesma corrente I e que os resistores em paralelo deve ter a mesma diferença de potencial ΔV.
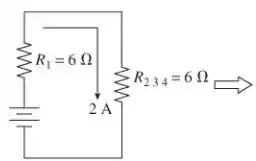
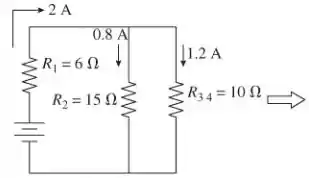
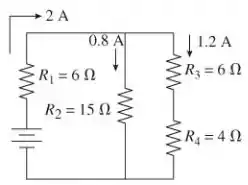
Na Etapa 1 da figura acima, = 12 Ω é retornado para = 6 Ω e = 6 Ω em série. Ambos os resistores devem ter a mesma corrente de 2,0 A que . Em seguida, usamos a lei de Ohm para encontrar
Como verificação, 12 V + 12 V = 24 V, que era ΔV do resistor . Na Etapa 2, a resistência é devolvida a e em paralelo. Ambos os resistores devem ter o mesmo ΔV = 12 V que o resistor . Então pela lei de Ohm
Como verificação, que era a corrente I do resistor . Na Etapa 3, é devolvido a e em série. Ambos os resistores devem ter os mesmos 1,2 A que o resistor . Em seguida, usamos a lei de Ohm para encontrar
Resposta
