Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 32.Exercícios e Problemas - Ex. 62
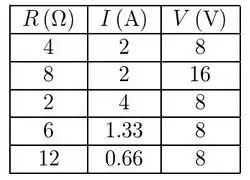
Para o circuito mostrado na FIGURA P32.62, determine a corrente e a diferença de potencial em cada resistor. Para facilitar a leitura, apresente seus resultados em uma tabela.
Passo 1
Se tivermos dois pontos e houver resistores conectados em ambas as extremidades dos pontos, chamamos de resistores conectados em paralelo. Isso é óbvio quando os resistores estão alinhados lado a lado. A diferença de potencial entre os resistores é a mesma na conexão em paralelo. A Equação (28.24) mostra a resistência equivalente para a conexão paralela na forma
Os dois resistores 6Ω e 12Ω estão em paralelo, então usamos a equação (1) para obter sua combinação por
Passo 2
Os resistores 4Ω estão em série com a combinação , então eles têm a mesma corrente. Aplicamos a regra do loop para obter a corrente através dos resistores 4Ω e a combinação . Viajamos no sentido horário no loop esquerdo e obtemos o próximo
Aplique a regra do loop no loop direito e viaje no sentido horário para obter
Passo 3
A corrente I é igual a . Usando essa relação na equação (2),
por isso, a corrente através de é
Use a lei de Ohm para obter a tensão em ambos os resistores por
A corrente I é a mesma para resistores 2Ω , então a corrente através dele é calculada por
Use a lei de Ohm para obter a tensão neste resistor por
Ambos os resistores 6Ω e 12Ω têm a mesma tensão e sua corrente de combinação é a mesma para , então usamos a lei de Ohm para obter a tensão em ambos por
Novamente usamos a lei de Ohm para obter a corrente através de 6Ω e 12Ω por
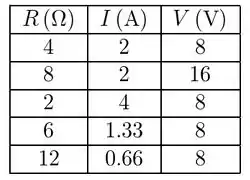
Resposta
