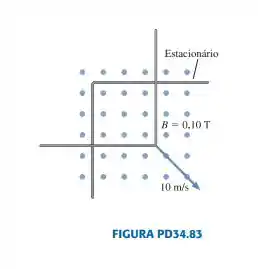
O condutor em forma de L da FIGURA PD34.83 move-se a próximo a outro condutor estacionário, também em forma de L, em presença de um campo magnético de . Em os dois vértices coincidem de forma que a área encerrada é nula. O condutor tem uma resistência de ohms por metro.
- Qual é o sentido da corrente induzida?
- Obtenha expressões para a fem induzida e para a corrente induzida como funções do tempo.
- Calcule e em
Passo 1
Faaaaaala, galera... Tranquileba??
Para a)
Vemos que o campo está saindo da página, então o fluxo está crescendo para forma conforme a espira expande. De acordo com a lei de Lenz, a corrente induzida tenta prever a o crescimento de fluxo para fora, isto faz gerar então um campo dentro da pagina, para isto requer uma corrente em sentido anti-horário.
Bora pro próximo passo?!
Passo 2
Para b)
Tomemos e por definição:
E nesse caso sendo constante:
E seja a espira regida por
Mas x:
E dado que:
Onde o ângulo é para onde x está crescendo, onde por estar perfeitamente na diagonal de uma espira quadrada. Assim:
E logo a área da espira:
E portanto:
E para a corrente sabemos que:
Mas a resistência de somente um lado da espira cresce com o tempo também, conforme x cresce, e em toda a espira é 4 vezes um lado da pira. De forma que:
Assim:
Passo 3
Para c)
Com
E como a corrente não depende do tempo:
Resposta
Para a)
Sentido horário
Para b)
Para c)
Para