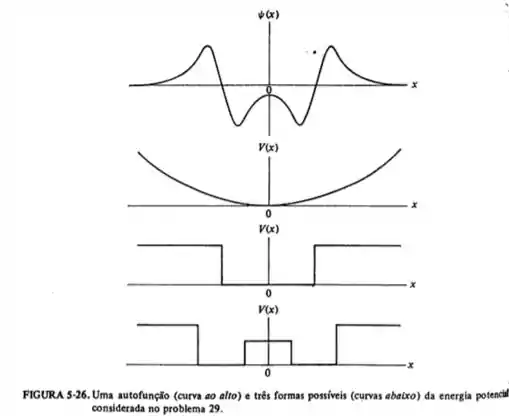
Considere a autofunção ilustrada na parte superior da figura 5-26. (a) Qual dos três potenciais ilustrados na parte inferior da figura poderia levar a tal autofunção? (b) A autofunção mostrada não é a correspondente ao estado de menor energia possível para o potencial. Trace um esboço da forma da autofunção que corresponde à menor energia. (c) Indique em outro esboço o intervalo de energias no qual você esperaria estados de energia possíveis discretos e o intervalo de energias no qual você esperaria que os estados de energia possíveis fossem distribuídos continuamente.
Passo 1
Fala galerinha, beleza?
Temos que identificar qual dos três potenciais corresponde melhor à função de onda fornecida.
Observe que conforme , a função onda decai exponencialmente. Lembre-se que a equação de Schroedinger pode ser escrita como
Se o potencial fosse o da primeira figura, teríamos (portanto ) conforme . Isso faria com que tivéssemos algo do tipo
A solução dessa equação corresponde a um decaimento exponencial, o que bate muito bem com a função de onda. Todavia, na região próxima de , o comportamento deveria oscilatório, o que claramente não verificamos já que ela se comporta de um jeito bem esquisito.
Por outro lado, o comportamento de decaimento exponencial para é condizente com as duas figuras de baixo se a energia for inferior aos potenciais limites:

Além disso, o comportamento esquisito da função de onda é condizente com a saliência presente na região central da última figura. Com isso, o potencial que melhor descreve a função de onda é o terceiro!
Passo 2
Para discutir o estado fundamental (de mais baixa energia) do sistema, temos que considerar um nível de energia como mostrado a seguir:
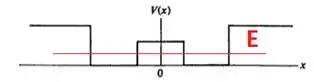
Nesse caso, a partícula tende a ficar restrita a um dos “mini poços”. O comportamento da função de onda vai ser oscilatório dentro deles:
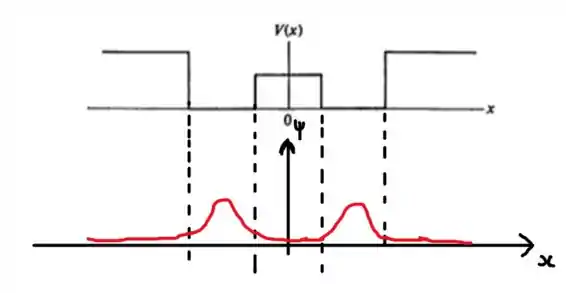
Passo 3
Com relação aos intervalos de energia discreta e contínua, basta verificar se temos um estado ligado ou não:
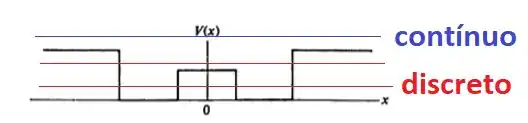
Resposta
Discussão e esboço.