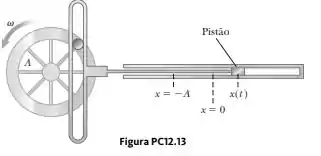
Considere o motor simplificado de pistão único na Figura PC12.13. Supondo que a roda gire com velocidade angular constante, explique por que a haste do pistão oscila em movimento harmônico simples.
Passo 1
Faaala, cara!! Tranquileba?
Antes de iniciar, façamos menção da equação do Movimento Harmônico Simples:
Tendo isto em mente, vamos analisar o problema :P
Passo 2
Analisando a imagem, podemos projetar a posição de um ponto da roda em coordenadas polares, ou seja, e tomando a equação do Movimento Uniforme (MU) da cinemática angular, temos:
Passo 3
Tendo isto em mente, para
E por que fizemos Pois, a amplitude é máxima quando a roda está a uma distancia R presa ao pistão.
Resposta
Respostas nos passos.