As equações listadas na Tabela 2.2 (volume 1) fornecem a posição como função de tempo, velocidade como função de tempo e velocidade como função de posição para um corpo movendo-se em linha reta com aceleração constante. A quantidade aparece em todas as equações. (a) Algumas dessas equações são aplicáveis ao corpo movendo-se em linha reta com movimento harmônico simples? (b) Usando um formato semelhante, faça uma tabela de equações descrevendo o movimento harmônico simples. Inclua equações que fornecem aceleração como função de tempo e aceleração como função de posição. Mencione equações que sejam igualmente aplicáveis a um sistema bloco-mola, a um pêndulo e a outros sistemas vibratórios. (c) Que quantidade aparece em todas as equações?
Passo 1
Alô Alô...
Arrasta pra cima e vamos desvendar esse mistériooo aiii..
As equações para o movimento em uma direção quando a aceleração é constante.
Passo 2
- No movimento harmônico simples, a aceleração é uma função da posição (quanto mais longe da posição de equilíbrio, maior a força restaurativa), logo nenhuma das equações citadas são aplicáveis para um movimento harmônico simples.
- As equações requisitadas pelo exercício são:
- A quantidade que aparece em todas as equações é a frequência angular .
Passo 3
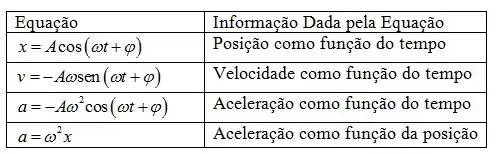
Todas as equações podem ser utilizadas em qualquer sistema vibratório, respeitando-se a especificidade de
Passo 4
Resposta
Vide a explicação no passo a passo.