Considere uma partícula se movendo sob influência do potencial , onde é uma constante, que está ilustrado na figura 5-21.
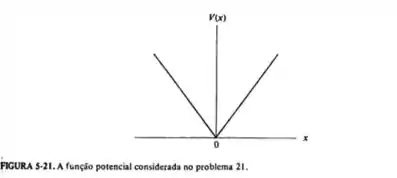
a) Use argumentos qualitativos, bastante semelhantes aos do exemplo 5-12, para fazer um esboço da primeira autofunção e da décima autofunção para o sistema.
b) Faça um esboço das duas funções densidade de probabilidade correspondentes.
c) Use então a mecânica clássica para calcular, da forma feita no exemplo 5-6, as funções densidade de probabilidade previstas por esta teoria.
d) Trace um gráfico das funções densidade de probabilidade clássicas juntamente com as funções densidade de probabilidade quânticas.
Passo 1
Fala galerinha, beleza?
Começamos escrevendo a equação de Schroedinger independente do tempo:
Substituindo , temos
O comportamento qualitativo vai ser determinado pela diferença de energia .
Para , o comportamento da função de onda é oscilatório, enquanto para , o comportamento passa a ser um decaimento exponencial. Assim, para tal que , a função de onda oscila e para , ela decai exponencialmente até para .
Para entender melhor o comportamento oscilatório, basta lembrar que o n-ésimo estado tem nós. Portanto, a primeira autofunção tem nós, enquanto a décima autofunção tem nós. Assim, podemos fazer o esboço das autofunções :
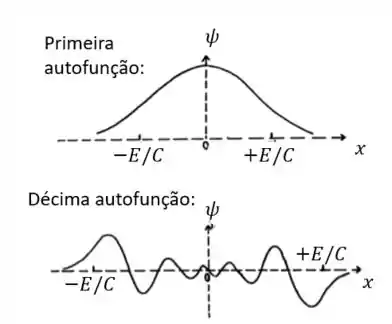
Observe que a primeira autofunção não corta o eixo por não apresentar nenhum nó. O movimento oscilatório ocorre apenas entre .
Passo 2
Para as densidades de probabilidade, basta tomar o quadrado da função de onda. Qualitativamente, isso significa rebater a parte negativa das funções de onda para cima do eixo :
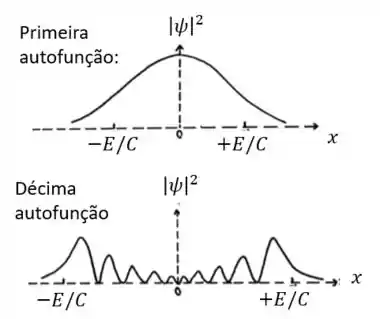
Passo 3
Como discutido no exemplo 5-6 do livro, a densidade de probabilidade clássica é dada por
A conservação de energia nos dá
Assim,
Para achar a constante de normalização , fazemos
Classicamente, os valores de e ocorrem quando :
Assim,
Como o integrando é uma função par:
Observe que como estamos integrando num intervalor com , fiz a substituição . Desta forma, temos
Ou ainda,
Portanto,
A seguir plotamos essa distribuição de probabilidades:
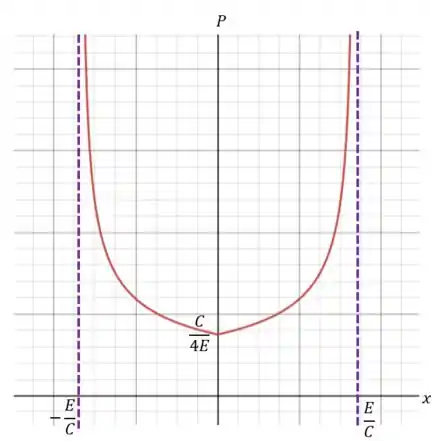
Resposta
Esboço de gráficos.