Considere o potencial função delta dobrado:
Na qual e são constantes positivas.
- Esboce esse potencial.
- Quantos estados ligados a equação possui? Calcule as energias permitidas, para e para , e esboce as funções de onda.
Passo 1
E aí, tranquilo? Para resolver o item a) basta esboçar o gráfico. Como consiste em uma função delta dobrada, teremos dois poços. Portanto, o gráfico fica:
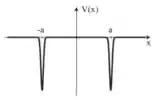
Com os picos em .
Passo 2
Agora para o item b), vamos analisar as soluções e buscar os estados ligados. Já vimos no Problema que as funções de onda sempre podem ser expressas como funções pares ou funções ímpares. Portanto, buscando primeiramente por soluções pares, vamos escrever as soluções em cada região como:
Da continuidade da função de onda em , podemos tirar que:
Ou seja:
Além disso, da descontinuidade da derivada no ponto , temos:
Essa relação ocorre devido ao potencial. Agora, para e , vem:
Podemos deixar essa igualdade mais organizada:
Assim, como temos em função de , vem:
Isolando a exponencial, temos:
Passo 3
Essa equação que obtivemos nos daria os valores de para os quais teríamos estados ligados. Porém, essa equação é transcendental e, portanto, não pode ser resolvida analiticamente. Contudo, podemos esboçar os gráficos das funções em cada lado da equação e buscar por intersecções. Definindo e , temos que as funções a serem plotadas são:
Assim, graficamente, temos:
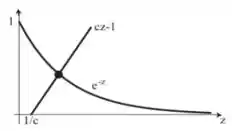
Note que temos apenas uma intersecção, portanto, temos apenas um estado ligado!
Passo 4
Buscando agora por soluções ímpares, temos:
Do mesmo modo que anteriormente, da continuidade em , encontramos:
Da descontinuidade da derivada da função de onda em , podemos encontrar:
Ou ainda:
Das duas equações para e , temos:
Passo 5
Resolvendo graficamente dessa vez também, podemos obter as seguintes soluções, definindo e da mesma forma que anteriormente:
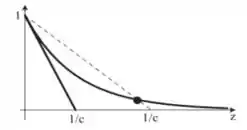
Note que há sempre uma intersecção dos gráficos em , contudo, esse ponto não é um estado ligado pois a função de onda não poderia ser normalizada com . Assim, nos resta apenas analisar a existência de outra interseção. Ela ocorre se for suficientemente pequeno para que a derivada da reta seja, em módulo, menor que a da exponencial. Ou seja, se:
Com isso, podemos concluir que, se , teremos dois estados ligados (um para a solução par e outro para a ímpar) e, se , teremos apenas um estado ligado relacionado à solução par.
Passo 6
O esboço das funções de onda par e ímpar, respectivamente, são os seguintes:
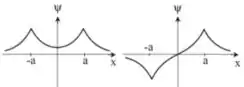
Passo 7
Por fim, as energias podem ser obtidas com o auxílio de uma calculadora. Para , temos que , assim, as soluções para são:
Portanto, as energias são:
Já para , . Assim, só temos uma solução . A energia associada fica:
Resposta
Se , teremos dois estados ligados (um para a solução par e outro para a ímpar) e, se , teremos apenas um estado ligado relacionado à solução par.
Para :
Para :