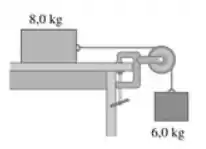
Considere o sistema indicado da Figura abaixo. A corda e a polia possuem massas desprezíveis, e a polia não possui atrito. O coeficiente de atrito cinético entre o bloco de 8,0 kg e o topo da mesa é dado por μ =0,250. Os blocos são liberados a partir do repouso. Use métodos de energia para calcular a velocidade do bloco de 6,0 kg no momento em que ele desceu 1,50 m.

Temos dois tipos de energia atuando: a energia cinética e a energia potencial em ambos lados. Então:

Como a questão fala que não há atrito na polia, o único coeficiente de atrito que deve ser levado em consideração é do bloco maior com a superfície.

Igualando as duas equações já que ambas tratam de energia:

A velocidade dos blocos é a mesma, logo v1 = v2 temos:

Agora é só substituir, resolver a questão e ser feliz!