Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 6.Problemas - Ex. 60
Por que a seguinte situação é impossível? Em um cassino novo, uma máquina de pinball superdimensionada é apresentada. A publicidade do cassino alardeia que um jogador de basquete profissional pode deitar sobre a máquina e a cabeça e os pés dele não ficarão para fora da beirada! O lançador de bola na máquina manda bolas de metal para cima em um lado da máquina e depois entra em jogo. A mola do lançador (Fig. P6.60) tem uma força constante de 1,20 N/cm. A superfície na qual a bola se move é inclinada = 10,0° em relação à horizontal. A mola é inicialmente comprimida em sua distância máxima d = 5,00 cm. Uma bola de massa 100 g é projetada no jogo pela liberação do êmbolo. Os visitantes do cassino acham o jogo da máquina gigante bastante excitante.
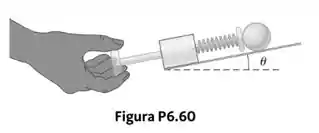
Passo 1
Pra gente verificar a impossibilidade dessa situação, vamos começar por determinar a altura máxima que a bola alcança, ao ser lançada pela mola, considerando que ela não bata em nenhum obstáculo.
A situação é mais ou menos essa:
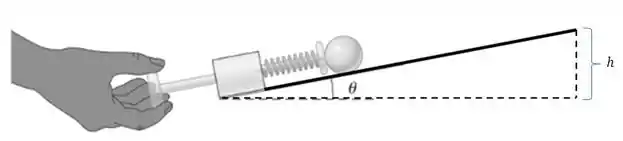
Se a gente considerar válida a conservação de energia, podemos estabelecer que a energia potencial da mola vai se converter totalmente em energia potencial pra bola quando ela chegar na altura .
Matematicamente, a gente tem:
Vamos determinar , isolando-o de um lado da igualdade e, considerando , a gente vai ter:
A gente pode converter (newton) assim:
Jogamos isso na equação, ficando com isso aqui:
Passo 2
Se a gente tem o ângulo e o cateto oposto a esse ângulo com tamanho , a gente consegue determinar a hipotenusa do triângulo retângulo, que equivaleria exatamente ao comprimento total da plataforma do Pinball “superdimensionado”.
Fazemos isso por trigonometria, usando a relação .
Uma vez que , por uma calculadora, a gente verifica facilmente que:
Assim, a gente pode escrever o seguinte:
Ou seja, gente, se a plataforma do pinball tem esse comprimento, em centímetros ainda, como é que um jogador profissional de basquete (que costumam beirar ou até ultrapassar os ) vai deitar sobre ela sem que seu corpo fique pra fora?
Loucura total!!
Resposta
Vide Passo 2.