Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 12.Problemas - Ex. 4
A constante solar, a intensidade da radiação solar que atinge a atmosfera terrestre, vale por minuto.
a) Quais são os valores máximos de e correspondentes?
b) Sabendo que o raio do Sol é de , e que a distância média Terra-Sol é , qual é a intensidade da radiação na superfície do Sol (supondo a emissão isotrópica e desprezando perdas)?
Passo 1
Legal, sabemos da equação 12.5.18 que a intensidade é o módulo da média do vetor de Poynting, de modo que
onde é a amplitude do campo elétrico:
Note que
Portanto, nosso objetivo no item (a) é encontrar !
Passo 2
Foi dado que intensidade da luz solar na Terra é
Vamos converter isso para :
Desta forma,
Com isso,
Fazendo as contas:
Assim,
Portanto,
Passo 3
Agora queremos achar a intensidade da luz solar na superfície do Sol. Consideremos o esquema:
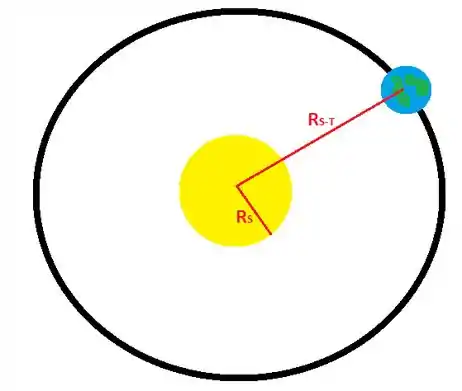
A luz emitida pelo Sol viaja esfericamente de forma igual em todas as direções. Desprezando perdas de energia, a potência na superfície do Sol é igual a potência distribuída na esfera de raio , onde está a Terra:
Mas sabemos que
Portanto,
Portanto,
Logo,
Com isso,