Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 12.Problemas - Ex. 2
Um fio condutor retilíneo cilíndrico muito longo, de condutividade e raio , transporta uma corrente constante, de densidade uniformemente distribuída sobre a secção transversal. Tome o eixo do cilindro como eixo .
a) Calcule na superfície do fio;
b) Calcule o vetor de Poynting na superfície do fio;
c) Mostre que o fluxo de através da superfície de um trecho de comprimento do fio é igual à energia dissipada em calor pelo efeito Joule nesse trecho, por unidade de tempo.
Passo 1
Primeiro vamos desenhar um esquema do fio:
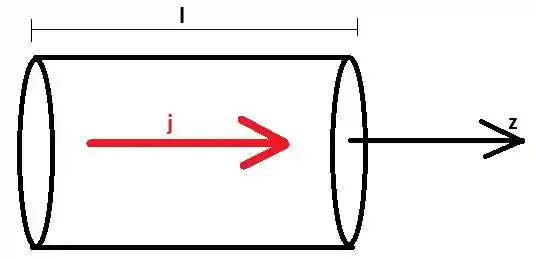
Para calcular o campo magnético na superfície do fio, usamos a lei de Ampére:
Aqui não precisamos adicionar a corrente de deslocamento pois não existe um campo elétrico variável no tempo que não está associado a uma corrente física como no caso do capacitor. Considerando um circuito de raio que engloba o fio, temos que
Por outro lado:
Portanto,
Com isso,
Usando notação vetorial, temos que, na superfície do fio,
Passo 2
Agora vamos para o item (b). Queremos calcular o vetor de Poynting, dado por
Como
temos que
Como :
O vetor de Poynting aponta para dentro do fio na direção radial.
Passo 3
No item (c) temos que calcular o fluxo de sobre a superfície do fio:
Como é radial, temos que considerar apenas a a superfície lateral:
Note que a integral de é a área lateral do cilindro, dada por . Portanto,
Passo 4
Note que podemos escrever:
onde é a área da secção transversal do fio. Além disso, podemos escrever
Assim,
Mas como a resistência elétrica é
temos que
Isso significa que a potência elétrica que vem de fora, transportada pelos campos (vetor de Poynting) é dissipado dentro do fio por efeito Joule:
Isso é mais um exemplo lindo de conservação da energia!