Enunciado
Física - Griffiths - Mecânica Quântica- Ed: 2º - Capítulo 2.Problemas - Ex. 10
a) Construa .
b) Esboce , e .
- Verifique a ortogonalidade de , e por meio de integração explícita.
Dica: Se você explorar a paridade e a imparidade das funções, restará apenas uma integral a ser obtida.
Passo 1
Fala aí, beleza?? Para começar a resolver esse problema, vamos utilizar o operador escada para sairmos do estado fundamental até o estado . Lembrando que vale a relação:
Assim, para o item (a), temos:
Abrindo as contas, chegamos em:
Ou seja:
Aplicando o operador novamente:
Desenvolvendo, temos:
Então...
Com isso, a função de onda é:
Passo 2
Agora, para resolvermos o item b), com o auxílio de um programa, podemos encontrar os seguintes perfis para as curvas , e :
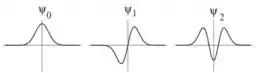
Passo 3
Por fim, vamos resolver o item c), verificando a ortonormalidade das funções , e .
Podemos notar que, como e são funções pares e é uma função ímpar, as integrais seguintes se anulam automaticamente:
Dessa forma, precisamos calcular apenas a integral seguinte:
Explicitando as funções, temos:
Desenvolvendo, chegamos em:
Essas duas integrais são integrais Gaussianas, portanto, tabeladas. Resolvendo as integrais, chegamos no resultado:
Assim, como a integral resultou em zero, as funções e são ortonormais, como já esperávamos!