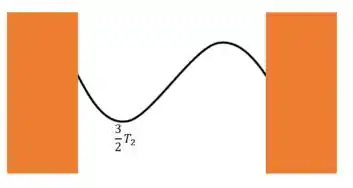
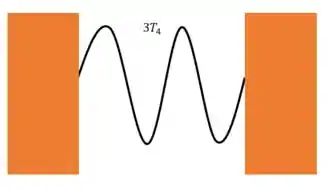
Uma corda de e de comprimento é fixada em ambas as extremidades. Se a tensão aplicada à corda for de , é possível produzir uma onda sonora cuja decomposição em componentes de Fourier no instante é apresentada ao lado.

a) Desenhe o espectro de frequências deste som. Quais as harmônicas intermediárias que faltam?

b) Suponha que nestas mesmas condições a corda fosse substituída por outra de maior massa. Nesse caso, o que aconteceria às frequências do som produzido?

c) Mantendo a corda inicial e aumentando a tensão, o que aconteceria às frequências do som produzido?

d) Desenhe a forma das ondas componentes para o instante , sendo o período da fundamental

A velocidade de propagação da corda vai ser

Belezinha, agora vamos lá resolver cada item separadamente :D

a) Vamos encontrar as frequências de cada componente mostrada na figura. Primeiro para a frequência fundamental (a que está com maior amplitude):

Substituindo e :

Agora a segunda harmônica (na figura, é a de menor amplitude)

E por fim, a quarta harmônica, que é a componente com 5 nós:

E é isso aí! Podemos notar que está faltando a terceira harmônica né? Só temos a componente de 2 nós (fundamental), 3 (segunda harmônica) e 5 (quarta harmônica)

b) Vamos lá para uma análise matemática:

O que acontece se aumentarmos a massa na fórmula de densidade, mantendo o mesmo comprimento ?

Bom, a densidade linear vai aumentar também, certo? São diretamente proporcionais

E o que acontece com a velocidade se a densidade linear aumentar?

A velocidade vai diminuir, porque a densidade está no denominador, são inversamente proporcionais

Por fim, se a velocidade diminuir, o que vai acontecer com a frequência?

Como a velocidade está no numerador, a frequência vai diminuir tambémmm

Ou seja: aumentar a massa da corda nos leva a diminuir todas as frequências

c) Legal, agora estamos aumentando a tensão mas mantendo a mesma corda lá do enunciado

O que acontece com a velocidade se a tensão aumentar?

A velocidade aumenta também, porque a tensão está no numerador

Se a velocidade aumentar, o que acontece com as frequências?

Como a velocidade está no numerador, a frequência vai aumentar também, certo?

Então, aumentar a tensão nos leva a um aumento das frequências :D

d) O período da fundamental é

O período da 2ª harmônica é

Então

E o período da 4ª harmônica é

Então

Agora sim, vamos pensar no problema hehehe

Queremos desenhar as componentes em

- Para a componente de frequência fundamental

Cada vez que a corda sobe e desce, ao chegar lá em cima de novo ela vai completar um período . Vamos dividir esse ciclo que ela faz em 4 vezes:

Quando ela chega lá embaixo, ela está na metade do período , em . No meio, ela passa por na ida e na volta

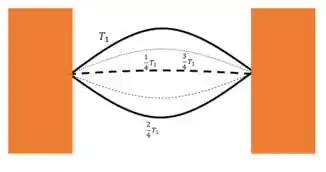
Então, em ela vai estar no meio:

- Para a segunda harmônica

Temos que

Então, em estamos falando de

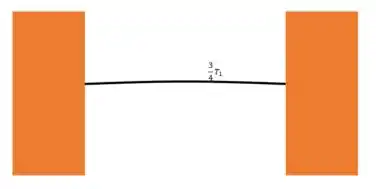
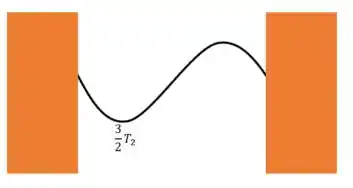
Vamos dividir o ciclo da segunda harmônica em duas partes: em , a onda vai estar na metade do seu período, ou seja, os picos vão estar invertidos. Em , ela vai ter completado um ciclo completo, voltando como estava em

Então, em , a corda vai estar com os picos invertidos, na metade de um período

- Para a quarta harmônica

Temos que

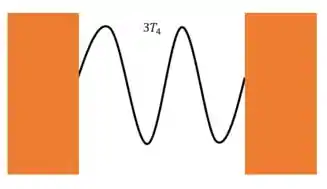
Então, em estamos falando de

Ou seja, simplesmente se passaram 3 períodos da quarta harmônica. Ao final de cada período, a onda está onde estava em , certo? Dessa forma, a quarta harmônica vai permanecer da forma que temos na figura do enunciado

E acabaaaamossss! Sobrevivemos galera hahahahaha