Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Oscilações, Ondas e Termodinâmica- Ed: 5º - Capítulo 13.Problemas - Ex. 18
Uma corda leve com uma massa por unidade de comprimento de 8,00 g/m tem as suas extremidades amarradas a duas paredes separadas por uma distância igual a três quartos do comprimento da corda (Fig. P13.18). Um corpo com massa m é suspenso a partir do centro da corda, colocando nela uma tensão. (a) Encontre uma expressão para a velocidade da onda transversal na corda em função da massa do corpo pendurado. (b) Qual deve ser a massa do corpo suspenso na corda, se a velocidade da onda for 60,0 m/s?
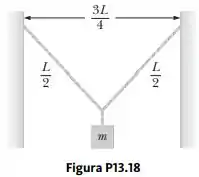
Passo 1
Fallaaaa ai galerinha, bora pra mais uuuum!!
- Usando a 2ª lei de Newton, aplicando a um corpo em repouso, sabemos que a tração aplicada ao bloco pendurado para esse exercício é de
- Para uma velocidade de 6,00 m/s, a massa do corpo é
Sendo m a massa do bloco, g a aceleração da gravidade, e o ângulo formado em razão da seguinte configuração:
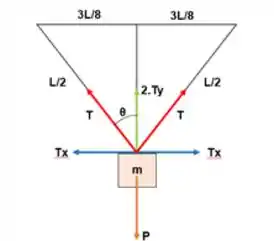
Ao substituirmos cada valor, obteremos a seguinte configuração para a tensão na corda:
Passo 2
A velocidade transversal na corda tem relação matemática bem definida, quando a trabalharmos em função da massa do corpo, para esta questão, obteremos o seguinte:
Passo 3
Temos que a massa do corpo é de 0,04 kg.
Resposta
Vide a explicação.