Uma corda com massa m = 8,00 e comprimento L= 5,00 m tem uma extremidade presa a uma parede. A outra extremidade é drapeada sobre uma roldana pequena, fixada a uma distância d = 4,00 m da parede e presa a um corpo pendurado de massa M = 4,00 kg, como na Figura P14.21. Se a parte horizontal da corda for puxada, qual é a frequência fundamental de sua vibração?
Passo 1
Faaalaaaaaa papitooooo, rs!
Tudo bem galera??
Bora láa!!
Para encontrarmos a frequência fundamental de vibração da corda vamos utilizar a seguinte equação:
Então vamos precisar calcular o valor da velocidade . Vamos lembrar que, para ondas e uma corda, é válido a seguinte expressão :
Neste caso, T representa a tensão na corda devido ao corpo pendurado e representa a densidade linear da corda e é igual a: . Onde, representa a massa e L e o comprimento da corda.
Passo 2
Foram dados:
, temos:
Para calcular a tensão na corda, considere o seguinte diagrama de corpo livre:
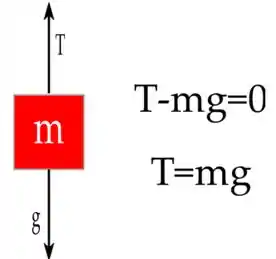
Passo 3
Assim, a velocidade será igual a :
E por ultimo
Resposta
Portanto, a frequência fundamental é de 19,56 Hz.