Uma corda da massa total m e comprimento L está suspensa verticalmente. A análise mostra que, para pulsos curtos transversais, as ondas acima de uma curta distância da extremidade livre da corda pode ser representada com uma boa aproximação pela equação de onda linear discutida na Seção 13.2. Mostre que um pulso transversal percorre o comprimento da corda em um intervalo de tempo dado aproximadamente por . Sugestão: Em primeiro lugar, encontre uma expressão para a velocidade da onda em qualquer ponto a uma distância x da extremidade inferior, considerando a tensão da corda como resultante do peso do segmento abaixo deste ponto.
Passo 1
Faaaaaalaaa galera, show de bolaa??
Arrasta pra cima e só vamoo!!
A situação do problema está representada na figura a seguir, em que a origem do eixo vertical (c=0) foi colocado na extremidade inferior da corda:
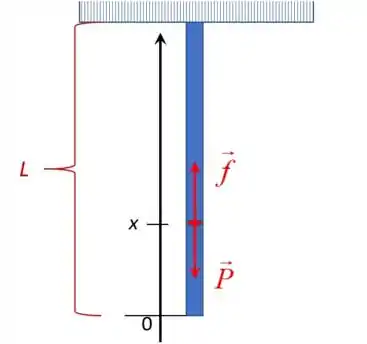
Em um ponto x qualquer da corda atuam duas forças: a força de tração de intensidade e a força peso, que atua na massa do segmento de corda suspenso abaixo do ponto x. Como esse ponto está em equilíbrio, teremos:
Em que é a densidade linear da corda.
Passo 2
A velocidade da onda que se propaga na corda será dada por:
Como , temos:
Passo 3
Integrando em ambos os lados da equação anterior, teremos:
Resposta
Vide a explicação.