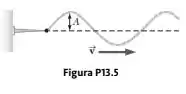
A corda mostrada na Figura P13.5 se propaga com uma frequência de 5,00 Hz. A amplitude

do movimento é de A=12,0 cm, e a velocidade da onda é v= 20,0 m/s. Além disso, a onda é tal que y=0 em x 0 e t=0. Determine; (a) a frequência angular e; (b) o número de onda para esta onda; (c) escreva uma expressão para a função de onda. Calcule: (d) a velocidade transversal máxima e; (e) a aceleração transversal máxima de um elemento da corda.

Logo, usando os dados enunciados no texto, temos:

O número de ondas:

E:

Logo:

Item c)

função

a função descrita como:

Tendo valores de , temos:

Item d)

Sabemos que a velocidade é a derivada da posição respeito ao tempo, logo:

E será máxima quando .

Assim

Item e)

Sabemos que a aceleração é a segunda derivada da posição respeito ao tempo, logo:

E será máxima quando

Assim: