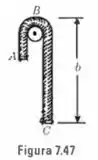
Uma corda uniforme ele massa M e comprimento L (Fig. 7.47 ) passa por um pino sem atrito e de raio muito pequeno. No início do movimento, B C =b . Mostre que a aceleração e a velocidade, quando B C = 2 / 3L , são a = g / 3 , v = 2 g / L( 8 3 L 2 + 2 b L - b 2 ) . Aplique os resultados obtidos a L = 12p é s é e b = 7p é s é .

Enunciado

E aí, beleza?? Vamos determinar a aceleração em um momento genérico, em que há uma porção do lado direito:

Portanto:

Quando , vem:

Aplicando a regra da cadeia, chegamos em:

Portanto:

Perceba que a expressão solicitada no enunciado está equivocada.

Numericamente, vem: