Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Mecânica- Ed: 2º - Capítulo 7.Problemas - Ex. 61

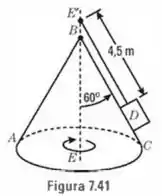
Um corpo D com 6   k g de massa (Fig. 7.41 ) está sobre uma superfície cônica A B C , sem atrito, girando em torno do eixo E E com velocidade angular de 10   r e v / m i n . Calcule: (a) a velocidade linear do corpo, (b) a reação da superfície no corpo, (c) a tensão no fio, e (d) a velocidade angular necessária para que a reação do plano seja zero.

Passo 1

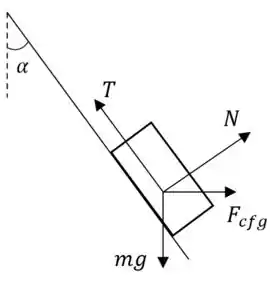
E aí, beleza?? O Diagrama de corpo livre do bloco, no referencial girante (isto é, considerando a força centrífuga), é:

Seja l o comprimento do fio que une o corpo ao topo do cone, então vem:

v = ω r = ω l   s e n α

Passo 2

Do equilíbrio de forças, decompondo nas direções paralela e perpendicular ao plano, vem:

N + m ω 2 r cos ⁡ ( α ) = m g   s e n α ∴ N = m   s e n α g - ω 2 l cos ⁡ ( α )

T = m g cos ⁡ ( α ) + m ω 2 r sen ⁡ ( α ) ∴ T = m g cos ⁡ ( α ) + ω 2 l sen 2 ⁡ ( α )

Passo 3

Para que a normal seja nula, vem:

N = 0 ∴ ω = g l cos ⁡ ( α )

Numericamente, as respostas são as seguintes:

Resposta

  1. v = 4,1   m / s

    3. N = 38,2 N

  3. T = 51,6 N

ω = 2,1   r a d / s  

Ver Outros Exercícios desse livro