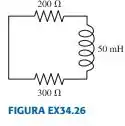
Em , a corrente no circuito da FIGURA EX34.26 é . Em que instante ela valerá ?

Faaaaaala, galera... Tranquileba??

Primeiro precisamos saber como é a equação do circuito RL, não?! Vamos lá!

Temos:

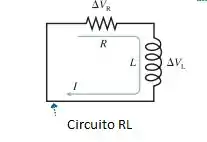
Pela lei de Kirchhoff, isto é:

Assim:

De modo que:

Integrando:

Onde, por definição da analise dimensionar deve ser dimensional, de forma que introduzimos um novo símbolo:

Com unidade de tempo.

Assim:

Com esse “insight” nem precisa mais de mim, né?! Mas se gosta de mim, cola pro próximo passo!