Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 32
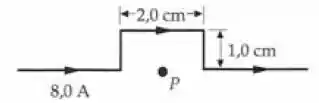
A corrente no fio mostrado na Figura 27-52 é . Determine o campo magnético no ponto P.
Passo 1
Olá pessoal, tudo certo com vocês? Espero que sim 😊. Vamos entender melhor essa questão?
Certo! Observe que os segmentos de corrente a-b e e-f não contribuem para o campo magnético no ponto P. A corrente nos segmentos b-c, c-d, e d-e resulta em um campo magnético em P que aponta para o plano do papel. Observe que os ângulos bPc e ePd são e use a expressão para devido a um segmento de fio reto para encontrar as contribuições para o campo em P dos segmentos bc, cd, e de.
Passo 2
No item a) como as correntes se repelem, elas são antiparalelas!
Passo 3
Sabemos que o campo magnético total é a soma das contribuições de cada campo individual, ou seja
Lembre-se que, a expressão para um campo magnético devido a um segmento de linha é dada por:
Passo 4
Perfeito! Agora vamos usar essa expressão, individualmente, de modo que, para e
Para
Passo 5
Somando todas as contribuições individuais, temos
Substituindo numericamente, encontramos que
para dentro da página.
Passo 6
Pronto! Finalizamos a questão 😊. Nos vemos na próxima questão. OK? Até mais.
Resposta
para dentro da página.