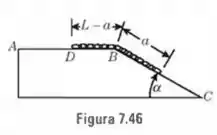
Uma corrente flexível de comprimento e peso (Fig.) é colocada inicialmente em repouso sobre uma superfície sem atrito . Inicialmente, a distância de a é . Prove que, quando a extremidade atinge o ponto , a velocidade da corrente é:
Passo 1
E aí, beleza?? Vamos calcular a aceleração da corrente:
Portanto:
Passo 2
Podemos reescrever a EDO da seguinte maneira:
Integrando, temos:
Ou seja:
Como queríamos demonstrar.
Resposta
Ei, a resposta está no passo a passo :)