Seu dedão range contra um prato que você acabou de lavar. Seus tênis rangem no piso do ginásio. Os pneus do carro chiam quando você põe em movimento ou para o carro abruptamente. Você pode fazer uma taça cantar passando seu dedo úmido pela sua borda. Quando um giz range no quadro-negro, você pode ver que ele faz uma série de traços regularmente espaçados. Como esses exemplos sugerem, a vibração geralmente resulta quando o atrito atua sobre um corpo elástico em movimento. A oscilação não é um movimento harmônico simples, mas conhecido como adere-e-desliza. Esse problema modela o movimento adere-e-desliza. Um bloco de massa m é preso a um suporte fixo por uma mola horizontal com constante de força k e massa desprezível (Figura P12.60). A Lei de Hooke descreve a mola tanto em extensão quanto em compressão. O bloco fica em uma placa horizontal longa, com a qual tem o coeficiente de atrito estático ms e um coeficiente de atrito cinético menor mk. A placa se move para a direita com ve locidade constante v. Suponha que o bloco passe a maior parte do tempo grudado na placa e se movendo para a direita com ela; então, a velocidade v é pequena em comparação à velocidade média do bloco conforme desliza de volta à esquerda. (a) Mostre que a extensão máxima da mola a partir da posição sem tensão é quase corretamente dada por ms mg/k. (b) Mostre que o bloco oscila ao redor de umaposição de equilíbrio na qual a mola é esticada por mkmg/k. © Trace o gráfico de posição versus tempo para o bloco. (d) Mostre que a amplitude do movimento do bloco é:
(e) Mostre que o período do movimento do bloco é
É quanto define o coeficiente estático em relação ao cinético que é importante para a vibração. “A roda que geme ganha a graxa”, porque um fluido viscoso não pode exercer uma força de atrito estática.
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer mais uma questãozinha aqui?
Vem comigo!
Letra a:
Passo 2
Letra b:
Conclusão: o bloco entra em movimento harmônico simples centrado sobre a posição de equilíbrio onde a mola é esticada por
Passo 3
Letra c:
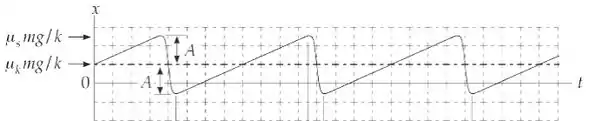
Passo 4
Letra d:
A amplitude de seu movimento é seu deslocamento original, , porque o bloco foi puxado para , então ele entra em movimento harmônico solar centrado sobre
Ele primeiro chega a descansar na extensão da mola:
Passo 5
Letra e: