Demonstre que deve exceder o valor mínimo de para cada solução normalizável da equação de Schrödinger independente do tempo. Qual é o equivalente clássico para essa afirmação?

Dica: Reescreva a equação na forma de:

Se , então e sua segunda derivada sempre têm o mesmo sinal; demonstre que tal função não pode ser normalizada.

A equação, reescrita da maneira do enunciado, fica:

Assim, se , então a diferença vai ser sempre um número positivo! Com isso, temos que e possuem o mesmo sinal! Você consegue visualizar o que isso significa graficamente?

Isso significa que, se o for positivo, sua concavidade também será e que, se for negativo, a sua concavidade também será negativa. A imagem a seguir ilustra isso:

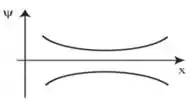
No entanto, para uma função ser normalizável, ela deve tender a zero nos limites . Dessa forma, essa função não pode ser normalizada, pois ela sempre tende a crescer cada vez mais, em módulo, quando tende aos infinitos.

O equivalente clássico é o seguinte: Podemos escrever a energia de uma partícula como a soma de sua energia potencial com sua energia cinética:

Assim, reorganizando a equação, o momento fica:

Ou seja, a energia deve ser sempre maior que o potencial , pois, caso contrário, o momento seria um número complexo! 😉