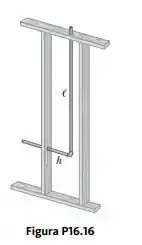
Dentro da parede de uma casa, uma seção em L do cano de água quente consiste em três partes: uma peça reta horizontal h = 28,0 cm de comprimento; um cotovelo; e um peça reta vertical l = 134 cm de comprimento (Fig. P16.16). Um cravo e uma tábua no segundo andar da casa mantêm essa seção do cano de cobre estacionária. Encontre o módulo e a direção do deslocamento do cano quando o fluxo de água é ligado, aumentando a temperatura do cano de 18,0 °C para 46,5 °C.
Passo 1
Falaaaaaaaaaaaaaaaa Tribuxo?
Bora resolver mais uma questão!?
Para resolver esse exercício iremos usar a seguinte equação:
Sendo
Segundo a tabela 16.1, temos:
Temos:
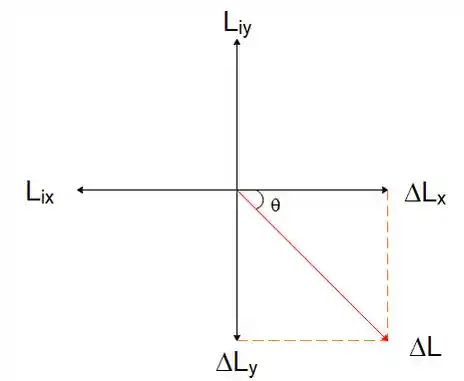
Precisamos achar o módulo e a direção do deslocamento do cano quando o fluxo de água, vamos desenhar:
Passo 2
Cada seção do tubo se expandirá separadamente, portanto, precisamos primeiro encontrar a mudança no comprimento em cada seção:
Substituindo:
Faremos o mesmo para :
Passo 3
Como estamos trabalhando com vetores, faremos:
Passo 4
Podemos achar a direção por:
Mandamos bem nessa!!!!!!
Até a próxima questão..............