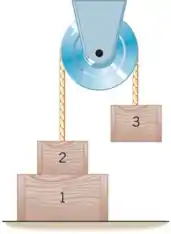
O desenho mostra a caixa 1 apoiada em uma mesa, com a caixa 2 apoiada no topo da caixa 1. Uma corda sem massa passa por uma polia sem massa e sem atrito. Uma extremidade da corda é conectada à caixa 2, e a outra extremidade está conectada à caixa 3. Os pesos das três caixas são W1 55 N, W2 35 N, e W3 28 N. Determine a magnitude da força normal que a mesa exerce na caixa 1.
Passo 1
Oiii, tudo certo?
Vamos lá resolver mais uma questão muito interessante para nosso entendimento completo do capítulo!
A figura que o problema dá é a seguinte
Passo 2
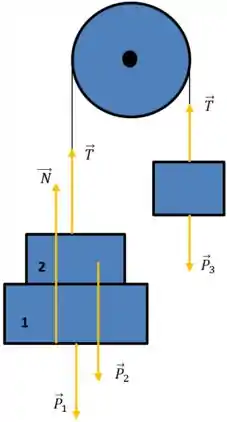
O desenho abaixo mostra as forças sobre caixas 1, 2 e 3. Uma vez que as caixas estão em repouso, elas estão em equilíbrio.
De acordo com a segunda lei de Newton, a força resultante na vertical, ou direção y, é zero
Existem duas incógnitas neste problema, a força normal () que a mesa exerce na caixa 1 e a tensão na corda () que conecta as caixas 2 e 3. Para determinar essas incógnitas, aplicaremos a relação de equilíbrio na direção duas vezes, uma vez para as caixas à esquerda da polia e uma vez para a caixa à direita.
Passo 3
Existem quatro forças agindo nas duas caixas da direita. As caixas estão em equilíbrio, então a força resultante deve ser zero. Escolhendo a direção como a positiva, temos que
Onde, e são os pesos das caixas, é a força normal que a mesa exerce na caixa 1, e é a tensão na corda. Nós sabemos os pesos.
Passo 4
Para achar a tensão , sabemos que a caixa 3 está em equilíbrio também, então a força resultante tem que ser zero.
Passo 5
Substituindo a expressão para na equação para o corpo em equilíbrio para as duas caixas à esquerda, e resolvendo para a força normal () temos que: