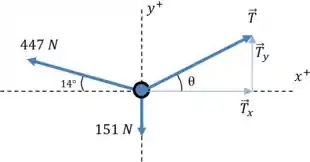
Durante uma tempestade, um galho de árvore quebra e cai em uma cerca de arame farpado cem um ponto que não está no meio entre dois postes de cerca. O membro exerce uma força descendente de 151 N no fio. A seção esquerda do fio faz um ângulo de 14,0 em relação à horizontal e sustenta uma tensão de 447 N. Encontre a magnitude e direção da tensão que a seção certa do fio sustenta.

Uma vez que o fio sob o membro está em repouso, ele está em equilíbrio e a força resultante agindo sobre ele deve ser zero.

Três forças compreendem a força resultante, a força de do membro, a força de tensão da seção esquerda do fio e a força de tensão da seção direita do fio.

Vamos dividir as forças em componentes e definir a soma dos componentes e soma dos componentes em , separadamente, e igualando a zero.

Então fazendo, vamos ter duas equações contendo as quantidades desconhecidas, que são as componentes horizontal e vertical da força de tensão . Estas duas equações serão resolvidas simultaneamente para fornecer valores para as duas incógnitas. Conhecendo os componentes de a força de tensão, podemos determinar sua magnitude e direção.

Tendo e sendo os componentes horizontal e vertical da força de tensão, respectivamente. O diagrama de corpo livre para o fio abaixo do membro é mostrado abaixo. Tomando como direções positivas, para a direita e para cima.

Fazendo a soma das forças na direção do eixo , temos que

Fazendo a soma das forças na direção do eixo , temos que

A magnitude da força de tensão é

Já que os componentes da força de tensão e o ângulo são relacionados por