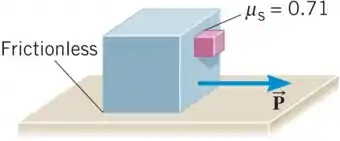
O desenho mostra um grande cubo (massa 25 kg) sendo acelerado através de uma superfície horizontal sem atrito por uma força horizontal. Um pequeno cubo (massa 4,0 kg) está em contato com a superfície frontal do grande cubo e deslizará para baixo, a menos que seja suficientemente grande. O coeficiente de atrito estático entre os cubos é 0,71. Qual é a menor magnitude que pode ter para evitar que o pequeno cubo deslize para baixo?

Os diagramas de corpo livre para o cubo grande (massa = ) e o cubo pequeno (massa = ) são mostrados nos desenhos a seguir.

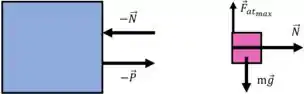
No caso do cubo grande, omitimos o peso e a força normal da superfície, uma vez que não desempenham nenhum papel na solução (embora eles se equilibrem).

Nestes diagramas, a gente pode ver que os dois blocos exercem uma força normal um sobre o outro; o grande bloco exerce a força no bloco menor, enquanto o bloco menor exerce a força no bloco maior.

De acordo com a terceira lei de Newton, essas forças têm direções opostas e magnitudes iguais .

Sob a influência das forças mostradas, os dois blocos têm a mesma aceleração .

De acordo com a segunda lei de Newton para o bloco maior, temos que

E para o bloco menor, temos

Substituindo a relação obtida para a força normal na equação de equilíbrio da força resultante para a força no bloco maior

Para que o bloco menor permaneça no lugar contra o bloco maior, a força de atrito estático

deve equilibrar o peso do bloco menor, de modo que

Mas é dado por, onde, a partir da segunda lei de Newton, sabemos que . Assim, nós temos que

Usando este resultado na expressão para dá