Este problema usa os mesmos conceitos do Exemplo 17 de conceito múltiplo. No Problema 80, um homem de 85 kg planeja rebocar um avião de 109.000 kg ao longo de uma pista puxando horizontalmente por um cabo conectado a ela. Suponha que ele em vez disso, tenta o feito puxando o cabo em um ângulo de 9,0 acima a horizontal. O coeficiente de atrito estático entre seus sapatos e a pista é 0,77. Qual é a maior aceleração que o homem pode dar ao avião? Suponha que o avião esteja sobre rodas que giram sem qualquer resistência ao atrito.
Passo 1
Opaaa tudo bem?
Sugiro que você dê uma olhada lá no Exemplo de Conceito 17, depois volta aqui pra gente fazer junto o problema ta?!
Passo 2
Já que assumimos que não há força de atrito resistindo ao movimento, a única força horizontal agindo no avião surge por causa da tensão (magnitude = ) no cabo.
O avião (massa =) sofre uma aceleração horizontal causado pelo componente horizontal da força de tensão, onde é o ângulo que o cabo faz com a horizontal.
Da segunda lei de Newton, a aceleração do avião é
Passo 3
O diagrama de corpo livre é o seguinte
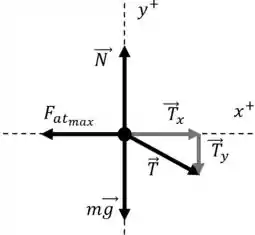
Passo 4
A tensão máxima no cabo é limitada pela condição que os pés do homem não devem escorregar.
Quando o homem puxa com muita força, sem escorregar, o componente horizontal da tensão agindo sobre ele corresponde ao atrito estático máximo força: (ver o diagrama de corpo livre do cara).
A força de atrito estática máxima em si é dada por . Juntas, essas duas relações produzem
Passo 5
Para avaliar a magnitude da força normal que atua sobre o homem, devemos considerar a Terceira lei de Newton. Esta lei indica que quando o homem (massa = ) puxa o cabo, o cabo puxa para baixo sobre ele.
Esta força para baixo aumenta a força normal para cima que a pista exerce sobre ele. Aplicando Segunda lei de Newton para a direção vertical neste diagrama, com aceleração zero, vemos que
Resolvendo para
Passo 6
Substituindo a equação para a força normal na equação obtida no Passo 4 temos
Resolvendo essa equação para temos
Passo 7
Substituindo a equação para a força normal na equação obtida no Passo 1 temos