Determine o ângulo entre dois vetores, de e unidades de comprimento, quando o vetor resultante faz um ângulo de com o vetor maior. Calcule, também, o módulo do vetor resultante.

E aí, beleza?? Vamos considerar a seguinte figura para nos basear para resolver esse problema:

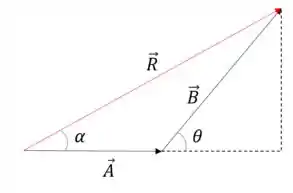
No problema, como o ângulo corresponde ao ângulo que o vetor resultante faz com o maior dos dois vetores, então e

Assim, da relação entre os lados e os ângulos demonstrada no problema 3, temos:

Portanto:

Assim: