Dois vetores, cujos módulos são de e unidades de comprimento, formam um ângulo de (a), (b) , (c) , (d) , e (e) . Determine o módulo da soma desses vetores e a direção do vetor resultante com relação ao vetor menor.
Passo 1
E aí, beleza?? Para resolver essa questão, considere a seguinte imagem:
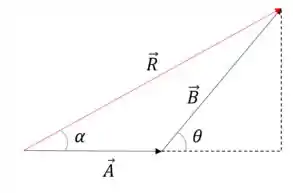
Vamos calcular de maneira genérica os resultados pedidos.
Para o módulo do vetor resultante, aplicamos a lei dos cossenos com o ângulo :
Logo:
Passo 2
Agora, para o ângulo , temos:
Logo:
Passo 3
Agora, aplicando os valores nos resultados obtidos, temos:
(a)
(b)
(c)
(d)
(e)
Resposta
(a)
(b)
(c)
(d)
(e)