Um diapasão gera ondas sonoras com uma frequência de 246 Hz. As ondas viajam em direções opostas ao longo de um corredor, são refletidas pelas paredes finais e retornam. O corredor tem 47,0 m de comprimento e o diapasão está localizado a 14,0 m de uma extremidade. Qual é a diferença de fase entre as ondas refletidas quando elas se encontram no diapasão? A velocidade de som no ar é 343 m/s.
Passo 1
Alô Alô, belezinha, encosta comigo que essa ta fácil...
Simborá moçadinhaaa
Para solucionarmos o problema, é necessário calcular a diferença de fase das ondas refletidas.
Vamos considerar o seguinte esquema:
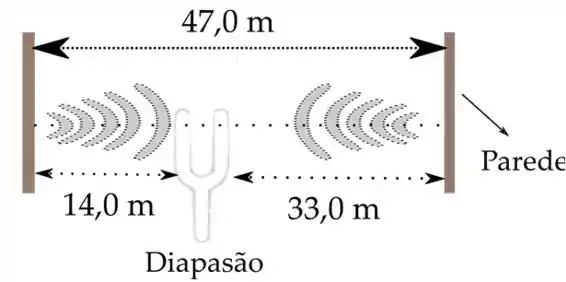
Passo 2
Vamos lembrar que a diferença de fase entre duas ondas relativamente a um determinado ponto é dado por:
Desta maneira, precisaremos tornar conhecido o comprimento de ondas, Sabemos que . Foi dado que e que . De maneira que o comprimento de onda será igual a:
Passo 3
Agora que conhecemos o valor do comprimento de onda, podemos calcular a diferença de fase. Vamos lembrar que e que . Desse modo, a diferença de fase será igual a:
Assim teremos:
Resposta
Portanto, a diferença de fase entre as ondas refletidas quando elas se encontram no diapasão é de 85.9 rad.