Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Exercícios - Ex. 1

Dois espelhos planos interceptam-se em um ângulo reto. Um feixe de laser atinge o primeiro deles em um ponto a 11,5 cm do ponto de interseção entre os dois espelhos, como mostrado na Figura 33.38. Que ângulo de incidência no primeiro espelho esse raio deve ter para atingir o ponto médio no segundo espelho (cujo comprimento é ) depois de se refletir no primeiro espelho?

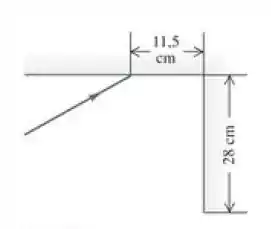
Passo 1

Queremos saber qual o ângulo de incidência do raio no primeiro espelho para que o raio atinja o ponto que está na metade do comprimento do segundo espelho, ok? Só que repara bem, o ângulo de incidência deve ser igual ao ângulo refletido, então o que temos é isso aqui:

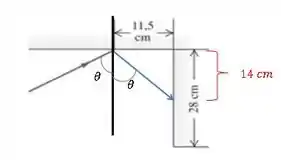
Show! Queremos saber o valor do para que essa situação occorra.

Passo 2

Olhando pra figura do passo anterior, temos que o ângulo que o raio refletido faz com a normal é um ângulo alterno-interno. Já que temos duas retas paralelas cortadas por uma transversal. Com isso, temos:

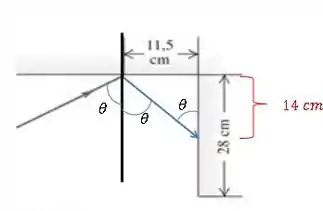
Maravilha!

Temos um triângulo retângulo. Podemos descobrir o nosso ângulo .

Calculando a tangente de :

Então

Show!!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 33-49 mostra um raio luminoso sendo refletido em dois espelhos perpendiculares A e B. Determine o ângulo entre o raio incidente i e o raio r ' .

Na Fig. 35-30, a onda luminosa representada pelo raio r , é refletida uma vez em um espelho, enquanto a onda representada pelo raio r 2 é refletida duas vezes no mesmo espelho e uma vez em um pequeno

Um raio de luz inicia no ponto ( - 2 m ,2 m ,0 m ) , incide em um espelho no plano y = 0 em algum ponto ( x ,0,0 ) e reflete através do ponto ( 2 m ,6 m ,0 m ) . (a) Determine o valor de x que torna m

Mostre que o ingulo de desvio 8e minimo se o angulo de incidenciaetal que o raio e a bissetriz do angulo de apice a(Figura31-62)se interceptam em angulos retos.