Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 31.1 - Ex. 84

Mostre que o ingulo de desvio 8e minimo se o angulo de incidenciaetal que o raio e a bissetriz do angulo de apice a(Figura31-62)se interceptam em angulos retos.

Passo 1

E aiiii gente, vem fazer essa questão tranquilíssima comigo!

Segura na minha mão, e vem!

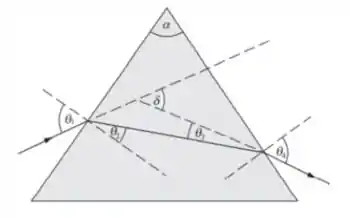
A figura abaixo mostra o prisma e o caminho do raio através dele. As linhas tracejadas são as normais para as faces do prisma. O triângulo formado pelo raio interno e as faces do prisma tem ângulos internos de α ,   90 º - θ 2 e 90 º - θ 3 . Consequentemente, θ 2 + θ 3 = α . Podemos aplicar a lei de Snell em ambas as interfaces para expressar o ângulo de desvio δ como uma função de θ 3 , e em seguida, definir a derivada desta função igual a zero para encontrar as condições em θ 3 e θ 2 que resultam em δ sendo um mínimo.

Passo 2

Expresse o ângulo de desvio:

δ = θ 1 + θ 2 - α                   ( 1 )

Aplique a lei de Snell para relacionar θ 1 com θ 2 e θ 3 com θ 4 :

sin ⁡ θ 1 = n sin ⁡ θ 2                   ( 2 )   e n sin ⁡ θ 3 = sin ⁡ θ 4                   ( 3 )

Resolva a equação (2) para θ 1 e a equação (3) para θ 4 :

θ 1 = s i n - 1 ⁡ n s i n ⁡ θ 2   e θ 4 = s i n - 1 ⁡ n s i n ⁡ θ 3

Passo 3

Substitua na equação (1) para obter:

δ = s i n - 1 ⁡ n s i n ⁡ θ 2 + s i n - 1 ⁡ n s i n ⁡ θ 3 - α = s i n - 1 ⁡ n s i n ⁡ θ 3 - α + s i n - 1 ⁡ n s i n ⁡ θ 3 - α

Observe que a única variável nesta expressão é θ 3 . Para determinar a condição que minimize δ , tome a derivada de δ   em relação a θ 3 e defina-a igual a zero.

d δ d θ 3 = d d θ 3 sin - 1 ⁡ nsin ⁡ θ 3 - α + sin - 1 ⁡ nsin ⁡ θ 3 - α = - n c o s ⁡ α - θ 3 1 - n s i n ⁡ α - θ 3 2 + n c o s ⁡ θ 3 1 - n s i n ⁡ θ 3 2 = 0   p a r a   o   e x t r e m o

Esta equação é satisfeita desde que:

α - θ 3 = θ 3 ⇒ θ 3 = 1 2 α

Como θ 2 = α - θ 3 :

θ 2 = α - 1 2 α = 1 2 α

Como θ 2 = θ 3 , podemos concluir que o ângulo de desvio é mínimo se o raio passar pelo prisma simetricamente.

Resposta

Ver resolução

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 33-49 mostra um raio luminoso sendo refletido em dois espelhos perpendiculares A e B. Determine o ângulo entre o raio incidente i e o raio r ' .
Mostre que, quando um espelho plano é girado por um ângulo θ em torno de um eixo no plano do espelho, um feixe de luz refletido (a partir de um feixe incidente fixo) que é perpendicular ao eixo de rot
Use a Figura 31-59 para calcular os ângulos críticos para a luz inicialmente em um vidro tipo silicato que incide na interface vidro-ar se a luz é (a) violeta com comprimento de onda 400 nm e (b) verm
Um raio de luz inicia no ponto ( - 2 m ,2 m ,0 m ) , incide em um espelho no plano y = 0 em algum ponto ( x ,0,0 ) e reflete através do ponto ( 2 m ,6 m ,0 m ) . (a) Determine o valor de x que torna m